1, 2, 4, 8, 16, 32, 64, 127, 254, 508, 1016, 2032, 4064. 8128. Ten en cuenta que los números perfectos son aquellos números enteros positivos que son iguales a la suma de sus divisores propios (excluyendo al propio número). Hasta ahora, solo se han descubierto 51 números perfectos, y los cuatro primeros se encuentran en la tabla de arriba.. El más pequeño de los números perfectos es el que acabamos de citar, el 6: Divisores propios de 6: 1, 2, 3, y se tiene que 1 + 2 + 3 = 6. El siguiente es el 28, y a ellos le siguen el 496 y el 8128. Los que se enumeran a continuación son los ocho primeros números perfectos conocidos: 6, 28, 496, 8128, 33550336, 8589869056, 137438691328.

TeoríA De NúMeros

¿Para Qué Sirven los Números Perfectos en Matemáticas?
Los números perfectos Periódico El Regio

Números Perfectos en Rango Euler y Euclides Función EsPerfecto Pseint 029 YouTube

numero perfecto

TeoríA De NúMeros
¿Para Qué Sirven los Números Perfectos en Matemáticas?

Diagrama de Flujo 10 Determinar si un Número es Perfecto YouTube
¿Cuál es el Número Perfecto? Universo Masseffect

Determinar números perfectosVisual Basic 2010 YouTube

Números perfectos qué son, para qué sirven y cómo se formulan Meteorología en Red

Numeros perfectos del 1100

Números perfectos. Qué son y cómo encontrarlos.

CUANDO UN NÚMERO ES CUBO PERFECTO , EJERCICIO RESUELTO YouTube

QUE ES UN NÚMERO PERFECTO.docx Matemáticas discretas Conceptos matemáticos

Matemático explica qué son los NÚMEROS PERFECTOS y por qué son básicos para nuestra vida YouTube

TeoríA De NúMeros
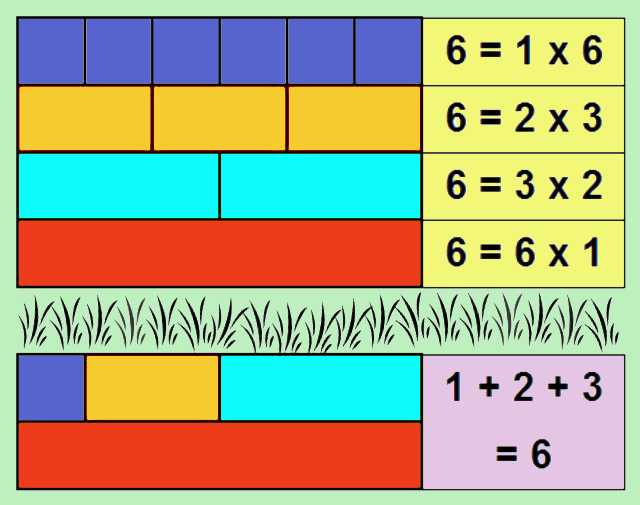
Números perfectos cómo identificarlos y ejemplos

El numero perfecto 9 YouTube

TeoríA De NúMeros
Los números perfectos de Euclides son todos números pares porque uno de los factores es una potencia de 2. Pero no hay evidencia para probar que no hay números perfectos impares; Todos los números perfectos conocidos terminan en 6 o 28, pero no siempre es así; Tampoco se ha probado que efectivamente existan infinitos números perfectos.. Los números perfectos son aquellos que son iguales a la suma de sus divisores propios. Un divisor propio de un número es cualquier número que divide al número de manera exacta, excepto el mismo número. Por ejemplo, los divisores propios del número 6 son 1, 2 y 3, ya que 1 x 6 = 6, 2 x 3 = 6.